Après une description de la plateforme expérimentale que représente le modulateur spatial de lumière et de son pilotage à distance, des courtes propositions de TP sont faites.

Le symbole ♣ marque des tâches expérimentales à suivre pour poursuivre les objectifs des TP.

Principe de la modulation spatiale de lumière

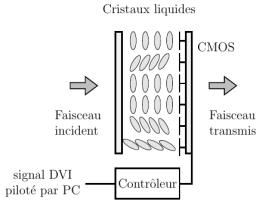
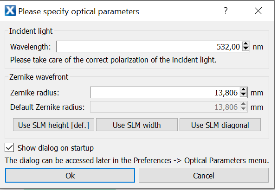
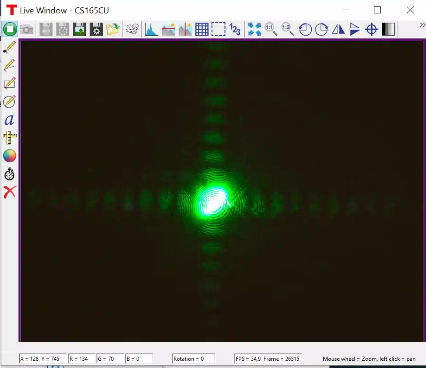
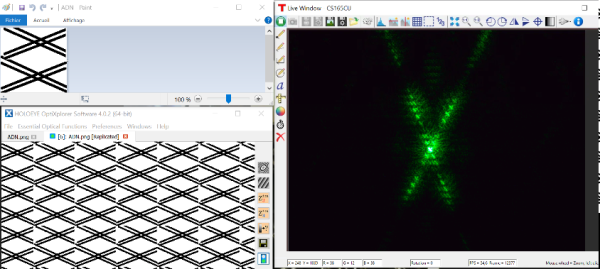
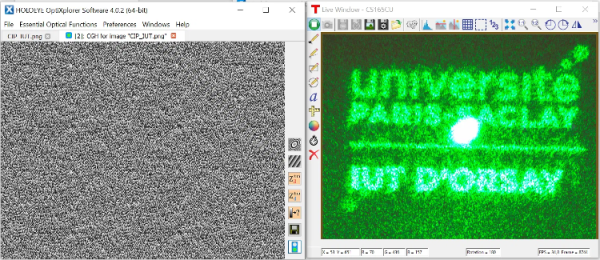
La manipulation consiste à piloter un écran à cristaux liquides à transmission pour générer une pupille d'étude et observer, dans le plan de Fourier, la figure de diffraction d'un faisceau laser vert à la longueur d'onde $\lambda =532\,\mathrm {nm}$ à travers cette pupille.

Cet écran pilotable a une résolution de 1024 x 768 et des pixels carrés d'une taille de 36 µm. Il rafraîchit à 60 fps et chaque pixel admet 256 niveaux de gris (codage 8 bits).

L'écran à cristaux liquides est appelé modulateur spatial de lumière ou SLM (pour spatial light modulator).

... (à venir)...

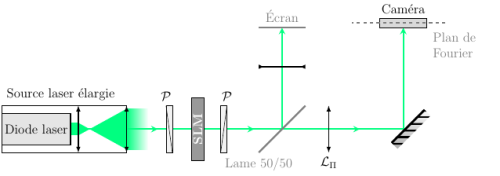
Le schéma optique est le suivant...

... (à venir)...

Connexion et manipulation distante

Se connecter à la station de travail pcj218-18, lancer l'utilitaire SLM.exe situé dans le dossier T:\Mphy\Cartable\TP_SLM.

Description de l'utilitaire

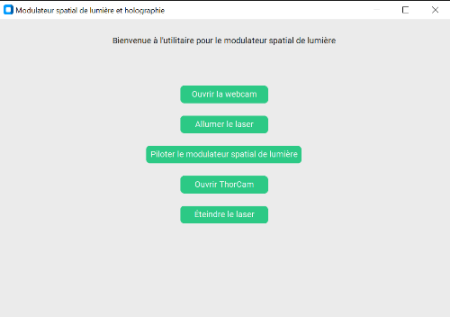
L'utilitaire SLM.exe est simplement constitué de 5 boutons permettant de lancer des raccourcis vers les différentes applications utiles à la manipulation à distance. Les 4 premiers boutons sont à déclencher dès le démarrage de la manipulation et le dernier ne doit pas être oublier lorsqu'on quitte.

Ouvrir la webcam : permet d'observer l'expérience, l'écran image de la pupille et visualiser l'éclairage, grâce à un flux vidéo lancé dans le navigateur web.
Allumer le laser : permet, en lançant une page php dans le navigateur web, de commuter l'interrupteur de la prise connectée pour que le laser et l'éclairage d'observation s'allument.
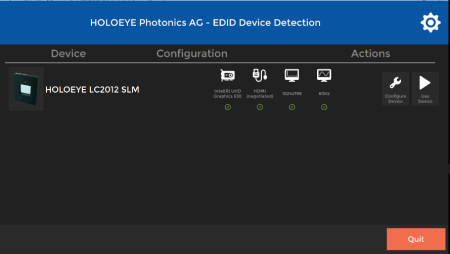
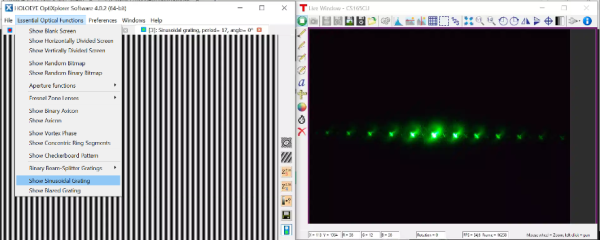
Piloter le SLM : lance l'application du constructeur Holoeye pour commander l'écran avec de nombreuses fonctionnalités.
Ouvrir ThorCam : lance l'application du constructeur Thorlabs pour capturer l'image et l'analyser.
Éteindre le laser : permet, en lançant une page php dans le navigateur web, de commuter l'interrupteur de la prise connectée pour que le laser et l'éclairage d'observation s'éteignent.

Logiciel Holoeye de pilotage de l'écran

Truc 1
Truc 2
Truc 3

Logiciel Thorlabs d'observation du plan de Fourier

Avertissement

Pour éviter toute surchauffe du système, il faut impérativement éteindre le laser après l'utilisation.

TP - Diffraction par une pupille quelconque

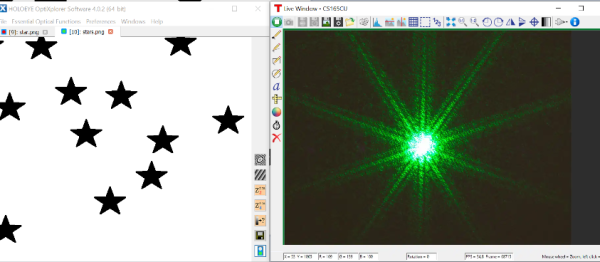
Dans l'application Holoeye, n'importe quelle image peut être ouverte, convertie en niveaux de gris et envoyée sur l'écran SLM.

♣ Ouvrir Paint ou n'importe quel autre logiciel de dessin et esquisser l'allure d'une pupille d'intérêt.

♣ Dans Holoeye, ouvrir cette image et, si sa résolution le suggère, la répliquer sur tout l'écran du SLM à l'aide du bouton à droite de l'outil de dé-zoom.

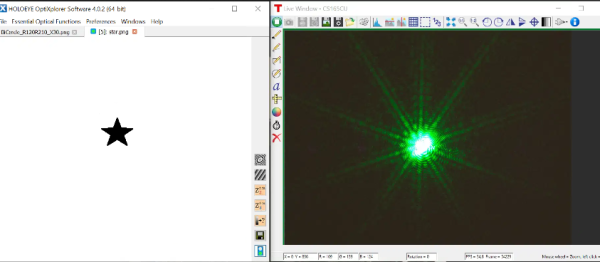
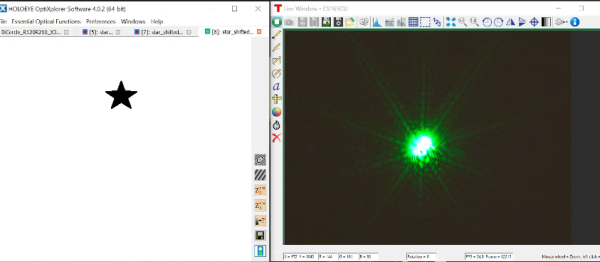
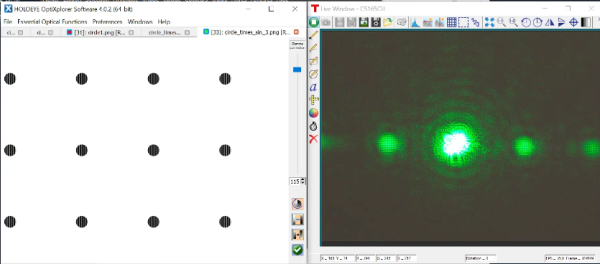
Un exemple

Simuler la diffraction par une molécule d'ADN

La découverte de la structure spatiale de l'ADN a été faite par diffraction de rayons X dans l'équipe de R. Franklin en 1952 au King's College de Londres. À l'aide de la démarche précédente, on peut repartir d'un modèle bidimensionnel de la double hélice (double croisillon) pour simuler la figure de diffraction qui est restée dans l'histoire comme le cliché 51.

♣ Reproduire ce travail de simulation du cliché 51.

♣ Changer les paramètres importants sur la figure, comme l'angle entre les croisillons ou le pas de l'hélice, l'épaisseur des brins, la distance entre ces derniers et en déduire leur influence sur la diffraction. Quel effet note-t-on entre la simulation avec un croisillon simple et un croisillon double ?

♣ Simuler l'influence des paires de bases azotées des nucléotides situées sur les deux brins complémentaires.

Principe de Babinet

Le principe de Babinet stipule que la figure de diffraction d'une pupille est identique à celle engendrée par la pupille complémentaire (en inversant parties opaques et parties transparentes), excepté pour l'intensité au voisinage immédiat de la direction donnée par l'optique géométrique. Il s'agit d'un théorème mathématiquement démontrable.

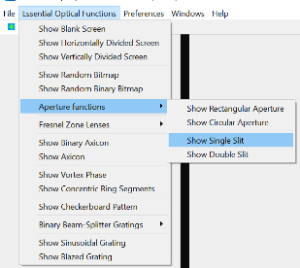
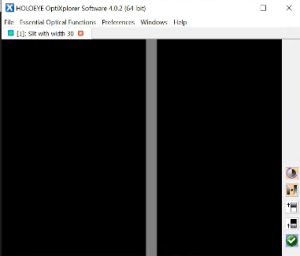
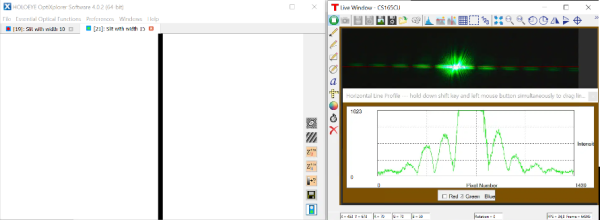
♣ Utiliser dans Holoeye la fonction optique essentielle de création d'une ouverture de type fente fine (essential optical functions>Aperture functions>show single slit). Choisir par exemple une largeur de 30 pixels. Observer sur Thorcam la figure de diffraction.

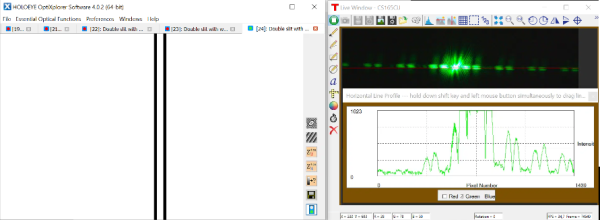
♣ Dans les outils de gestion du contraste au dessus du bouton "feu vert" d'affichage à l'écran du SLM dans Holoeye, utiliser l'inversion exact des valeurs (invert currently displayed bitmap). Observer l'effet sur la figure de diffraction et illustrer ainsi le principe de Babinet : un cheveu et une fente de même dimensions engendrent la même figure.

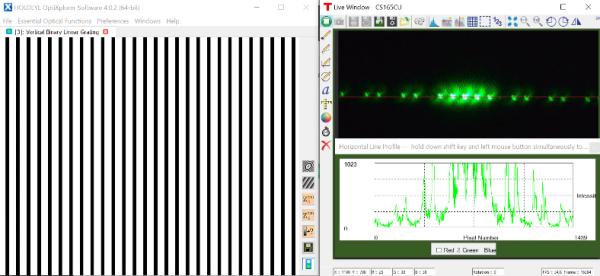
TP - De la diffraction par une fente aux interférences à N-ondes

♣

TP - Simulation de transformées de Fourier

Transformées de Fourier à deux variables

Soit une variable spatiale $x$ et sa variable réciproque (fréquence spatiale) $\nu$ . On appelle transformée de Fourier l'application :

$f(x)\,{\overset {\mathrm {TF} }{\mapsto }}\,{\widehat {f}}\left(\nu \right)=\int _{-\infty }^{+\infty }f(x)\,\mathrm {e} ^{-j\,2\,\pi \,\nu \,x}\,\mathrm {d} x\,.$

Cette transformée de Fourier se généralise à deux dimensions :

$f(x,y)\,{\overset {\mathrm {TF} }{\mapsto }}\,{\widehat {f}}\left(\nu _{x},\nu _{y}\right)=\iint _{-\infty }^{+\infty }f(x,y)\,\mathrm {e} ^{-j\,2\,\pi \,\nu _{x}\,x}\,\,\mathrm {e} ^{-j\,2\,\pi \,\nu _{y}\,y}\,\mathrm {d} x\,\mathrm {d} y\,.$

On montre que, dans l'approximation de Fraunhofer d'observation dans le plan focal d'une lentille convergente de focale $F$ , il existe un lien de transformée de Fourier entre le facteur de transmission $t\left(x,y\right)$ de la pupille créée sur le modulateur spatial de lumière et l'amplitude lumineuse diffractée au niveau du plan de Fourier. On a noté $(x,y)$ les coordonnées spatiales dans le plan du SLM. On note maintenant $(X,Y)$ les coordonnées au niveau du plan de Fourier. L'intensité lumineuse $I(X,Y)$ observée vérifie alors :

$I(X,Y)\propto \left|{\widehat {t}}\left({\frac {X}{\lambda \,F}},{\frac {Y}{\lambda \,F}}\right)\right|^{2}$ .

On remarque que les variables réciproques représentant des fréquences spatiales sont $\nu _{X}=X/(\lambda \,F)$ et $\nu _{Y}=Y/(\lambda \,F)$ .

Propriétés de la transformée de Fourier

Changement d'échelle

On a :

$f\left(T\times x\right)\,{\overset {\mathrm {TF} }{\mapsto }}\,{\dfrac {1}{T}}\times {\widehat {f}}\left({\dfrac {\nu }{T}}\right)$ .

Donc l'intensité observée dans le plan de Fourier après changement d'échelle sera proportionnel à $\left|{\widehat {f}}\left({\dfrac {\nu }{T}}\right)\right|^{2}$ .

♣

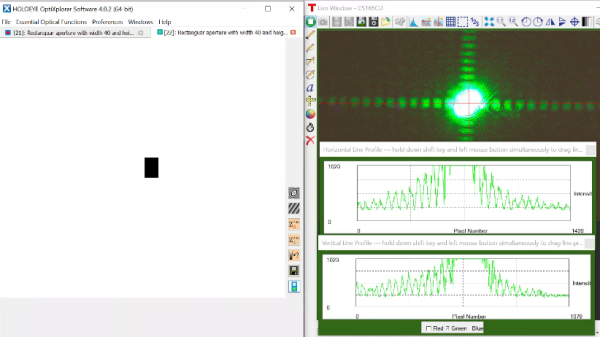
[[File:rectangle2_slm.png|border|600px|légende]

Translations

Dans l'espace direct

On a :

$f(x-a)\,{\overset {\mathrm {TF} }{\mapsto }}\,\mathrm {e} ^{-2\,j\,\pi \,a\,\nu }\times {\widehat {f}}\left(\nu \right)$ .

Donc l'intensité observée dans le plan de Fourier après translation de la pupille sera inchangée.

♣

Dans l'espace réciproque

On a :

$f(x)\cos \left(2\,\pi \,\nu _{0}\,x\right)\,{\overset {\mathrm {TF} }{\mapsto }}\,{\dfrac {1}{2}}\left({\widehat {f}}\left(\nu -\nu _{0}\right)+{\widehat {f}}\left(\nu +\nu _{0}\right)\right)$