Modulation spatiale de lumière

Principe de la modulation spatiale de lumière

légende

La manipulation consiste à piloter un écran à cristaux liquides à transmission pour générer une pupille d'étude et observer, dans le plan de Fourier, la figure de diffraction d'un faisceau laser vert à la longueur d'onde $\lambda =532\,\mathrm {nm}$ à travers cette pupille. Cet écran pilotable a une résolution de 1024 x 768 et des pixels carrés d'une taille de 36 µm. Il rafraîchit à 60 fps et chaque pixel admet 256 niveaux de gris (codage 8 bits).

Le schéma optique est le suivant...

légende

Connexion et manipulation distante

Se connecter à la station de travail pcj218-18, lancer l'utilitaire SLM.exe situé dans le dossier T:\Mphy\Cartable\TP_SLM.

Description de l'utilitaire

légende

Logiciel Holoeye de pilotage de l'écran

légende

légende

légende

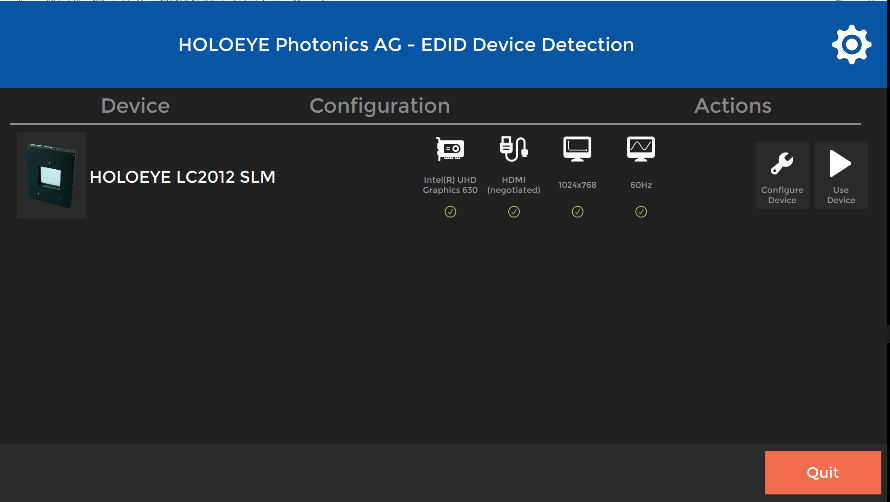
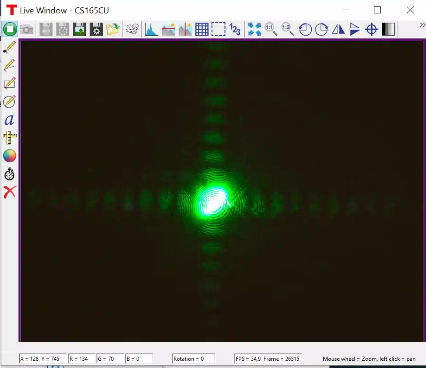
Logiciel Thorlabs d'observation du plan de Fourier

légende

légende

Avertissement

Pour éviter toute surchauffe du système, il faut impérativement éteindre le laser après l'utilisation.

TP - Diffraction par une pupille quelconque

légende

TP - De la diffraction par une fente aux interférences à N-ondes

légende

légende

légende

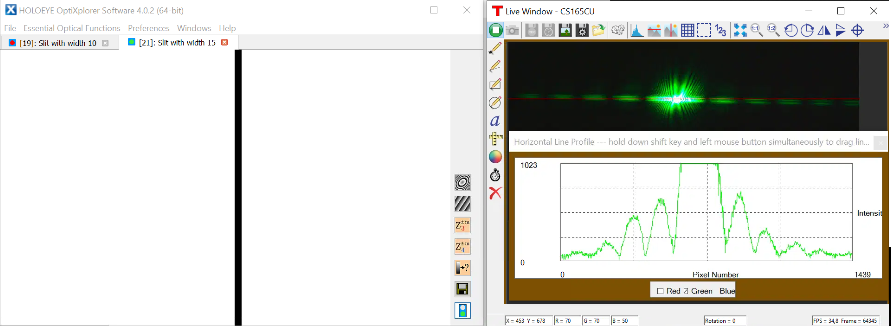
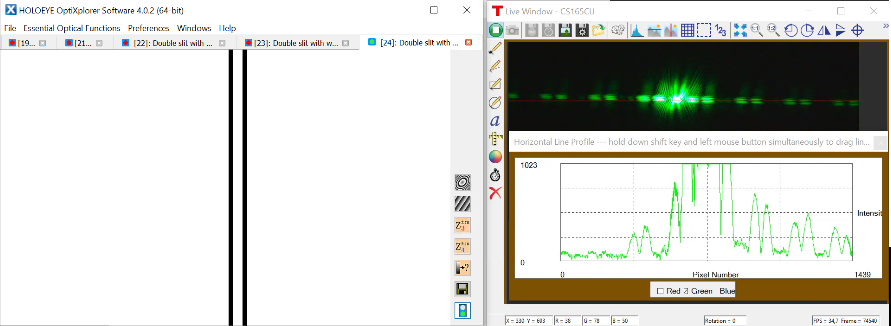
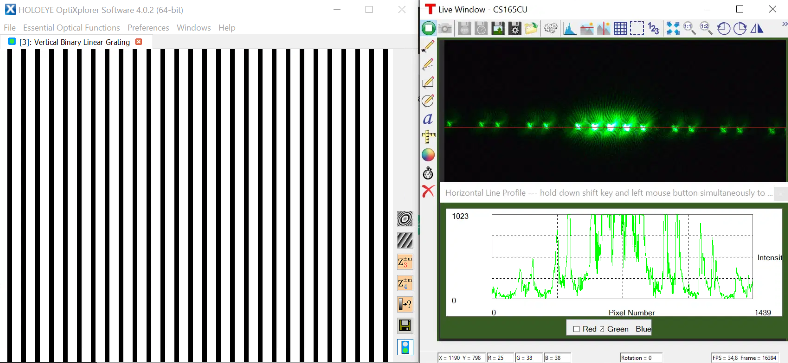
TP - Simulation de transformées de Fourier

Transformées de Fourier à deux variables

Soit une variable spatiale $x$ et sa variable réciproque (fréquence spatiale) $\nu$. On note la transformée de Fourier l'application :

$f(x)\,{\overset {\mathrm {TF} }{\mapsto }}\,{\widehat {f}}\left(\nu \right)=\int _{-\infty }^{+\infty }f(x)\,\mathrm {e} ^{-j\,2\,\pi \,\nu \,x}\,\mathrm {d} x\,.$

On montre que, dans l'approximation de Fraunhofer d'observation dans le plan focal d'une lentille convergente de focale $F$, il existe un lien de transformée de Fourier entre le facteur de transmission $t\left(x,y\right)$ de la pupille créée sur le modulateur spatial de lumière et l'amplitude lumineuse diffractée au niveau du plan de Fourier. Avec $(x,y)$ les coordonnées spatiales au niveau du SLM et $(X,Y)$ les coordonnées au niveau du plan de Fourier, l'intensité lumineuse $I(X,Y)$ observée vérifie alors :

$I(X,Y)\propto \left|{\widehat {t}}\left({\frac {X}{\lambda \,F}},{\frac {Y}{\lambda \,F}}\right)\right|^{2}$.

On remarque que les variables réciproques représentant des fréquences spatiales sont $\nu _{X}=X/(\lambda \,F)$ et $\nu _{Y}=Y/(\lambda \,F)$.

Propriétés de la transformée de Fourier

Changement d'échelle

On a $f\left({\dfrac {x}{T}}\right)\,{\overset {\mathrm {TF} }{\mapsto }}\,T\times {\widehat {f}}\left(\xi \times T\right)$. Donc l'intensité observée dans le plan de Fourier après changement d'échelle sera  $\left|T\right|^{2}\times \left|{\widehat {f}}\left(\xi \times T\right)\right|^{2}$.

Translations

Dans l'espace direct

On a $f(x-a)\,{\overset {\mathrm {TF} }{\mapsto }}\,\mathrm {e} ^{-2\,j\,\pi \,a\,\xi }\times {\widehat {f}}\left(\xi \right)$. Donc l'intensité observée dans le plan de Fourier après translation de la pupille sera inchangée.

Dans l'espace réciproque

$f(x)\cos \left(2\,\pi \,\xi _{0}\,x\right)\,{\overset {\mathrm {TF} }{\mapsto }}\,{\dfrac {1}{2}}\left({\widehat {f}}\left(\xi -\xi _{0}\right)+{\widehat {f}}\left(\xi +\xi _{0}\right)\right)$

Produit de convolution

$f\circ g\left(x\right)\,{\overset {\mathrm {TF} }{\mapsto }}\,{\widehat {f}}\left(\xi \right)\times \,{\widehat {g}}\left(\xi \right)$

Fonction stable par transformée de Fourier

légende

légende

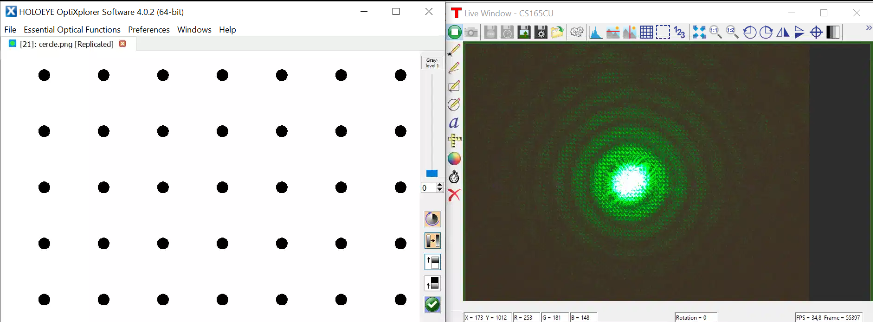
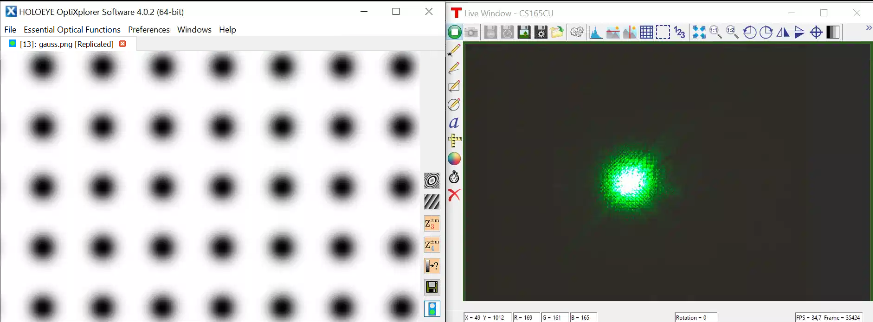
Échantillonnage

À venir

légende

TP - Holographie numérique

légende

légende

légende

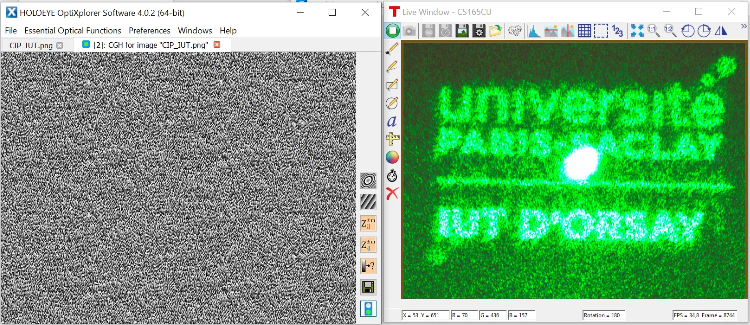
TP - Optique adaptative

À venir

Ressources pédagogiques

Les sujets de TP sont disponibles...